Rendering 3D Anaglyph in OpenGL - 2

since: 2013/08/22
update: 2013/08/29
reference:
0. 原文: Rendering 3D Anaglyph in OpenGL
1. I touchs: Rendering 3D Anaglyph in OpenGL - 1

E. 視差方程式:
      1. 之前提到, 視差可在品質上度量到. 現在開始要在位於某個深度的頂點, 引進視差
          的觀念來獲得方程式. 要畫出立體浮雕, 所需設定的 OpenGL 並不是重要的關鍵,
          重要的是在你的互動應用中, 所繪製的場景全部範圍都要使用合適的視差. 考慮
         下面的圖解, 其中, 頂點 V 位在深度 w, 並且是在收斂距離 C 再往後的地方:
     

                                  圖四: 測量位在收斂距離 C 後方的頂點 V 之視差值

      2. 兩眼間隔為 D, 收斂距離為 C. 連結左邊攝影機 L 與頂點 V 的線, 在收斂平面上
          相交為 P. 同樣地, 連結右邊攝影機 L 與頂點 V 的線, 在收斂平面上相交為 Q.

          與頂點 V 相關聯的視差距離 PQ 定義為 p(小p). 現在, 考慮三角形 LVR,
          從截線定理(intercept theorem)可以得到:

PQLR=VQVR

          類似地, 在三角形 QVM 與 VRN 中, 我們可以得到:

VQVR=VMRN=w−Cw=1−C/w

          因此, 

PQLR=pD=1−C/w

          或

p=D(1−C/w)

      3. 類似地, 下面的圖為比收斂距離更近的頂點: 

                                  圖五: 測量位在比收斂距離 C 更近的頂點 V 之視差值                                      

      4. 與頂點 V 相關聯的視差距離 PQ: p(小p), 可以再次套用截線定理獲得:

PQLR=QVVR=QVQR−QV=QVQR1−QVQR

           在三角形 QNR 中, 因為 VM 平行 RN, 因此:

QVQR=VMRN=C−wC=1−w/C

           因此,

PQLR=pD=1−w/Cw/C=C/w−1

           或,

p=−D(1−C/w)

      5. 這個方程式與位在收斂距離後方的頂點相同, 只差了一個負號. 負號意味著:
          收斂平面上的頂點投影, 相對於攝影機是在相反的一側. 如果忽視方程式中
          的正負符號, 負視差可以被理解成: 頂點開始移動得比收斂距離更近.
          p=D(1−C/w)可繪製成以下的圖:
 

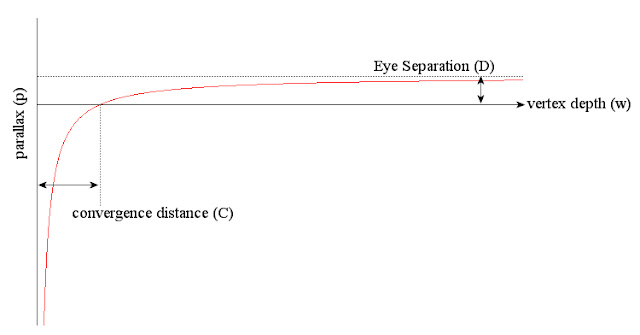
                                  圖六: 給定收斂距離與兩眼間隔, 頂點深度的視差變化量

      6. 圖中顯示, 當頂點移動越遠離場景, 所產生的視差越接近兩眼間隔 D.
          在收斂距離 C 的地方, 視差為零; 而所有深度大於收斂距離的頂點, 視差皆保持
          正值. 在場景中, 所有比收斂距離 C 更近的頂點, 視差為負值, 並且快速地接近
          無限大. 注意到, 當頂點的深度 w 等於 C/2 時, 所得到的視差值等同於兩眼間隔.
          過大的負視差, 會使觀察者的眼睛視線偏離, 而造成變形, 應該避免.
          根據攝影機的鏡頭與所要拍攝的效果(浮出螢幕或沈入螢幕)作為基準, 來選擇
          實用的收斂深度. 典型的兩眼間隔保持在收斂距離的 1/30, 並且在場景中,
          要避免讓物體近於收斂距離一半的位置上. (即: 深度不可小於 C/2 )