update: 2012/05/10
reference:
1. Nate Robins - OpenGL - Tutors
2. Tutorial 3 : Matrices | opengl-tutorial.org
3. 齊次座標
Transformation(轉換)
A. Homogeneous coordinates(齊次座標):
1. 齊次座標可以讓我們使用同一種數學方程式, 來對點(頂點)或向量處理:
平移, 縮放與旋轉的問題.
2. 在齊次座標中, 我們引入了 w 參數到原本三維的座標: (x, y ,z) 裡:
(x, y, z, w), w 代表座標軸的遠近參數. 要將齊次座標轉換為三維座標,
其方式為: (x/w, y/w, z/w).
3. (x, y, z, w) 在齊次座標中:
當 w == 1, 代表此為空間中的一個位置(點或頂點). => (x/1, y/1, z/1) = (x, y, z)
當 w == 0, 代表此為一個向量. => (x/0, y/0, z/0)
-------------------------------------------------------------------------------------
B. Transformation Matrices(轉換矩陣):
1. 矩陣介紹:
a. 簡單來說, 矩陣是一個在預先定義好列(row, 水平向)與欄(column, 垂直向)
的架構裡存放數值的陣列. 舉例: 2(row) x 3(column) 矩陣如下所示:
轉換 (x,y,z,w) 頂點:
(4x4)矩陣 x 頂點 = 轉換的頂點 (x', y', z', w')
****************************************************************
2. Identity Matrix(單位矩陣):
a. 說明: 在線性代數中, n 階單位矩陣, 是一個 n x n 的方形矩陣, 其主對角線元素
為 1, 其餘元素為 0.
b. 單位矩陣乘以任何座標(x, y, z, w), 其結果還是原始座標(x, y, z, w).
3. Translation Matrices(位移矩陣):
a. 位移矩陣如下所示, 其中 X, Y, Z 分別為各軸的位移量.
(備註: 在此 w = 1, 所以是頂點)
c. 接著, 來看看一個朝著負 Y 軸方向的向量 (0, 0, -1, 0), 往 X 軸方向位移 10 個
單位, 其結果會是如何? (備註: 在此 w = 0, 所以是向量)
****************************************************************
4. Scaling Matrices(縮放矩陣):
a. 縮放矩陣如下所示, 其中 X, Y, Z 分別為各軸的縮放比例.
(1). w 值不會變.
(2). 單位矩陣為縮放矩陣的特例, 當其縮放比例: (X,Y,Z) = (1,1,1).
(3). 單位矩陣亦為位移矩陣的特例, 當其各軸位移量: (X,Y,Z) = (0,0,0).
****************************************************************
5. Rotation Matrices(旋轉矩陣):
(圖片來源: 齊次座標)
****************************************************************
****************************************************************
6. Culumating Transformations(轉換計算):
a. 例如: 轉換的座標 = 縮放矩陣 x 旋轉矩陣 x 位移矩陣 x 原始座標
說明: 實際上矩陣相乘的順序為: 位移(先), 旋轉, 縮放(最後).
(從右到左, 離遠始座標最近的先計算)
b. 事實上, 以上的順序也是遊戲角色與其它物品常會使用到的:
先置放位置(位移), 然後改變方向(旋轉), 接著縮放大小(如果有需要的話).
-------------------------------------------------------------------------------------
C. The Model, View and Projection Matrices
1. 說明: Model, View 與 Projection(投影) 矩陣, 是一個可以用來清楚的區分轉換的方便工具.
****************************************************************
2. The Model Matrix:
a. Model Space:
所有的頂點是相對於此 model 的中心點而定義的, 亦即物件的中心點是 (0,0,0).
所有的頂點是相對於世界的中心而定義的.
3. The View Matrix:
a. Camera Space:
所有的頂點是相對於 camera 而定義的.

b. 最初 camera 是在 World Space 的原點(0,0,0), 我們可藉由移動 camera 來
相對的移動整個世界(從 camera 的觀點來看).
座標裡的 Model)向左 (負 X 軸) 移動 3 個單位.
d. 藉由 View Matrix, 我們將一個 Model 從 World Space 移到了 Camera Space.
****************************************************************
4. The Projection Matrix:
a. Homogeneous Space:
所有被定義在一個小立方體(cube)裡的頂點, 才會在螢幕上呈現.
b. 在 Camera Space 中, 座標為 (0, 0) 的點將會被畫在螢幕的中心.
c. Perspective Projection(透視投影):
我們不能只用 (x, y) 座標來決定物件擺放在螢幕的位置, 也要將物件到 camera
的距離(z)計算在內. 對於二個有相似 x, y 座標的頂點, 其中有較大 z 座標的頂點
(代表距離 camera 較近), 將會比另一個頂點更位在螢幕的中心處. 這就叫做
透視投影.
d. 最後, 藉由 Projection Matrix, 我們將一個 Model 從 Camera Space 移到了
Homogeneous Space.
D. The Transformation Tutorial Program
1. 開啓 I touchs: OpenGL: Nate Robins - Tutors 00 中調整好的專案, 將 active scheme 選為 transformation 後執行.
2. Translation(位移):
glTranslatef(X 軸位移量, Y 軸位移量, Z 軸位移量);
說明: 此處車子向正 X 軸位移 0.2 個單位;
相對的, camera 會向負 X 軸位移 0.2 個單位.
****************************************************************
3. Rotation(旋轉):相對的, camera 會向負 X 軸位移 0.2 個單位.
****************************************************************
glRotatef(旋轉角度, X 軸向量, Y 軸向量, Z 軸向量);
****************************************************************
glScalef(沿 X 軸的縮放係數, 沿 Y 軸的縮放係數, 沿 Z 軸的縮放係數);
說明: 此處沿 Z 軸放大 1.50 倍, 就像車子沿著正前方開過來.







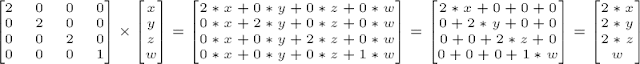











感謝您的文章,說明的非常清楚!
回覆刪除不客氣, 祝您學習順利!
回覆刪除